This entry goes out to all you amazing observers who want to do better science with your photometric data. Over on the AAVSO listervs I also see emails from folks asking for good comparison stars for variable stars, especially those one off variables – supernova and nova – that tend to go off once, or once in a lifetime. This discussion (based on the talk I gave at AstroFest Saturday) will help those of you wanting to come up with your own comp stars make the measurements you need.
For those of you not wanting to get into the special details of photometry, rest assured tomorrow I’ll have a special online treat 🙂
Now onto the the nitty-gritty data analysis details…
There are several different ways to obtain astronomical data. Perhaps the three most common forms of data are contour plots, spectra, and photometry. In each case the data has to be calibrated in a different way. While (IMHO) spectral data are perhaps the hardest to process and analyze, calibration often requires nothing more than looking at a flux standard and imaging a lamp or a series of lamps. At the other end of the spectra, photometric data is relatively easy to reduce and analyze, but calibration is a long and tedious project. This document attempts to explain the best way to make it through this long and tedious process, called All-Sky Photometry
I Why suffer?
No two data sets from two different telescopes can be assumed to be identical. Two diferent processes work against observers, changing measured values non-standard ways.
Airmass: The first problem is airmass. When an observer looks at an object straight overhead, the light they are observing passes through what is called 1 airmass of atmosphere. Along the way, that light will get thinned out by the atmosphere as photons are scattered through interactions with gas atoms/molecules. This process, called Raleigh Scattering, is responsible preferentially effects light (photons) with short wavelengths. In this way, sunlight passing through the atmosphere has its blue photons absorbed. those photons are then emitted in random directions (and perhaps re-absorbed and re-emitted multiple times). This process of absorption and re-emission is called scattering, and it leads to our sky being blue (which should give you a sense of how far across the atmosphere sideways a photon may end up going before it gets scattered toward an Earth-bound observer).
As an observer looks at objects lower and lower in the sky, they are viewing light that has had to travel through progressively more atmosphere. The more atmosphere the light from a source has to go through, the higher the probability the blue light (and maybe even the green and yellow light) from the object will be scattered out. This effect explains why the sky becomes more and more red as the Sun gets closer to the horizon. Scientifically, we refer to the amount of atmosphere the light must travel through as air mass, and mathematically, airmass =
(A good airmass calculator is here: AAVSO calculator)
In general, you don’t want to take data below an airmass of 1.2 (more than X degrees away from Zenith) because you’re fighting the atmosphere. Even within this window, however, airmass effects can alter the measured magnitude of an object by a few tenths of a magnitude. To determine how to correct for this loss of blue light, it is necessary to measure how the observed magnitude of known objects changes as a function of airmass. (More on this below.) Since stars of different colors will have their overall black body curve mutated in different ways (with blue stars getting more of their light knocked out than red stars), it is necessary to take calibration images in more than 1 filter.
Optical throughput: The second problem effecting photometric data is the variation in throughput of optical systems as a function of wavelength. Different mirror coatings, different lens coatings, and different glasses all reflect and transmit light in different ways at different wavelengths. For instance, check out this discussion on Silver versus Aluminum mirror coatings. By the time the light (or at least what’s left of it) reaches the detector, different chunks of the electromagnetic spectrum have been removed in part or in whole (this link shows you the curves for the Canada-France-Hawaii Telescope). Different detectors then do their own part to remove light, with CCDs being general less efficient detectors in the blue than in the red (see this discussion on back illuminated CCDs). This effect essentially acts like an additionally filter, and causes your telescope to respond in a non-standard way. To figure out how to correct for this problem, it is necessary to take images of objects spanning a wide range of colors and measure how the difference in published magnitude and measured magnitude deviates as a function of color. As with airmass, it is necessary to obtain calibration images in at least 2 filters.
II Observing Strategy
When trying to calibrate a scientific field it is necessary to set aside one photometric night (which ever one turns out to have the absolute cleanest skies), and spend an evening doing calibration images. A photometric night is defined as one in which the sky’s transparency is the same in all directions (typically, this means there are no clouds anywhere – it does not mean the seeing is good. It is alright to use a night with ok but not great seeing to do all sky photometry).
A list of papers containing primary standards and secondary standards (created using the primaries) is provided below. These objects have been selected to be non-variable and generally free of too-close neighbors. Primary standards can be thought of as the kilogram mass locked up in France from which the kilogram has been defined, and secondary standards can be thought of as uber expensive laboratory masses that have their masses defined using that kilogram mass in France.
In selecting standard fields, you want to choose fields that bracket your objects in airmass and containing objects that bracket your objects in color. In other words, If your object starts the evening with an airmass of 1.2, select comp fields that have airmasses of 1.4 and 1.0, as well as near 1.2. If your object has a B-V of between 0.2 and 1.2, your comparison objects you range from 0 to 1.4 (with a lot of colors in between). By extending the data you have for your comparison fields beyond your actual object, you can help guarantee the corrections you solve for are legitimate and eliminate the need for extrapolation. It is also useful to try and find standards close in magnitude to your science fields. The fainter you go, the harder this will be. As the exposure times of objects get longer, the variation in airmass from beginning to end of the exposure will increase. This isn’t a problem for similiar exposure tines, but things get messy when you are apply airmass term solved for using 5 second exposures to a 5 minute exposure.
My personal all sky photometry strategy is to sort my objects by RA and make a table of the time when the rise to an airmass of 1.2, the time they set through an airmass of 1.2 and what their minimum airmass is. I then add in standard fields that rise before my first object, set after my lasts object and fill in all the spaces in between. I will then observe on a rotation that allows me to follow my objects through the sky. (See example below).
There a couple important caveat: 1) Keep your standard fields as close to your science fields as possible, 2) Sometimes there just won’t be a standard field that reaches as high an airmass as your science field (this is because the standard fields are grouped around the equator and your objects probably aren’t. If you are observing near either pole, fields may not be available.)
It is more important than ever to obtain good bias, dark and flat exposures on the night you do all-sky photometry. Don’t forget that you’ll need darks (if your CCD requires them) for all the exposure times you use. If you have any concern that your CCD temperature is varying, take biases and darks throughout the night, interleaved with your observations. It is also good to take flats at the beginning and end of the night, to make sure no changes took place.
III Reduction Overview
This is not meant to teach data reduction. If you want to learn data reduction, go read this or this.
That said, here’s the “Quick Start” version.
1) Combine you bias exposures into a master bias using median combine
2) Subtract your master bias from everything
3) Examine your darks by exposure length. If they vary through the night, don’t combine exposures taken from different batches (but do median combine those from the same batch if you took more than.
4) Carefully subtract the master darks (or individual darks) from the images (flats and science frames) with the same exposure time taken at the same time of night.
5) Average combine your flats from the beginning and end of the night. Try subtracting 1 from the other. If you get a nice flat nothing, try combining average combining the flats from the beginning and end of the night.
6) Divide your science images by the master flats. If you have non-identical flats for the beginning and end of the night, you’ll have to do a bit of trial and error to figure out when the conditions changed.
7) Do NOT co-add anything.
8) Back up everything 🙂
IV Photometry
This can be done in many many different software packages. In general, you want to choose an aperture that is 4-6 times your average full width half max for the entire night. In general, a good way to determine the correct aperture for your image is to make a plot (for stars of many magnitudes) of (Magnitude / Magnitude with 1 pixel aperture) versus aperture for apertures ranging from 1 pixel to 8 x FWHM. The point where all the slopes go ~flat is a good aperture.
You will want to use the same aperture for all stars in all images. You may be tempted to not do this. Do not give into temptation! The FWHM of a star (not a galaxy / QSO / Planet / etc) is determined strictly by the atmospheric conditions. If you have a steady, photometric night, all stars of all magnitudes will have the same FWHM (within error). If this isn’t the case, your night isn’t suited for all-sky calibration photometry.
Once you have your data, organize it into columns along these lines:
| Object | Filter 1 | Filter 2 | ||||||
| Time | Airmass | mag | err | Time | Airmass | mag | err | |
(Example File here)
V Solving Transformations
So, now you have your data. That means it is time for math.
The generic equation for a transformation is:
where, m_B = instrumental magnitude in B, B = published apparent magnitude in filter B, x_1B = zero-point offset (the baseline difference between instrumental and published magnitudes, (x_2B) = airmass correction in Filter B, X_B is that observations airmass, (x_3B) = colour-term correction, and BR = B-R color.
If you have three filters, and the data for each filter has three unknowns, then you have three equations and 9 unknowns. You can’t solve that algebraically with just one observation! Instead, you have to fit a plane to the data using fancy statistical software (or IRAF), or you solve things iteratively using excel.
Here’s how. (I apologize for the graphics of the math).
At some point in your life someone probably taught you that the equation for a line is y=mx+b, where y=what you plot on the vertical axis, x=what you plot on the horizontal axis, m is the slop of the line through the data, and b is where that line intersects the vertical axis. Excel is capable of solving for the line that best fits a data set that has been plotted. (Just right click on data and select “Add Trendline”)
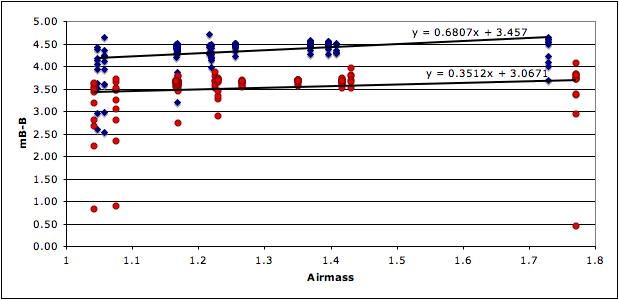
We’re going to start by assuming the colour term is close to zero and solve for the airmass term. Start by adding the published magnitudes to your spread sheet (as in the example), and creating a column for instrumental – published magnitude. Now plot (instrumental – published) versus airmass. The slope of this line is your first draft of the value for the airmass correction term (x2_F1). You can then use that value in the transformation equation to fit a line to the color term.
To solve for the color term, you want to now want to create a column in your table for (instrumental_F1 – actual_F1 – (x2F1)(airmass in F1) and plot it against the color (F1-F2). The slop of this line is now the colour term and the Y-intercept is a second draft of the zero-point offset.
You can now solve for the airmass term more accurately by making a new plot.
You cannot iterate a couple times between solving for the colour term and refining the airmass term.
To check your solutions, you need to invert the equations above to solve for the actual magnitudes using the instrumental magnitudes and coefficients. This is ugly if you try and solve for, say, B and R directly, but solving for R and BR is fairly straightforward. Take the equations for m_B and m_R and subtract them from one another and solve for BR first.
You should stop iterating your solution when the difference between the published BR & R and your calculated BR & R values stop improving.
VI Applying Transformations
Having checked your values for the standard stars against the published values, you now know your transformation works (and the stdev between calculated-published gives you your error). Now you can you the same inverted equations to solve for the values of your science targets and the secondary standards you use in your field (e.g. the comp stars in differential photometry).
Once you have good solutions for a variety of standards in your field, it is possible to use those secondary standards to determine the zero point offsets for future images taken on imperfect nights.
Standard Star Papers
- – Landolt, (1983) UBVRI photometric standard stars around the celestial equator
- – Landolt, (1992) UBVRI photometric standard stars in the magnitude range 11.5-16.0 around the celestial equator
- – Christian et al. (1985) Video camera/CCD standard stars (KPNO video camera/CCD standards consortium)
- – Odewahn et al. (1992) Improved CCD standard fields”

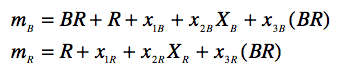
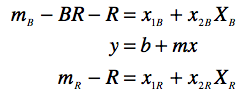
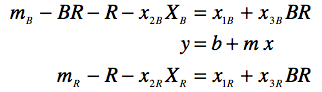
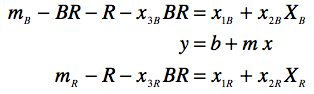
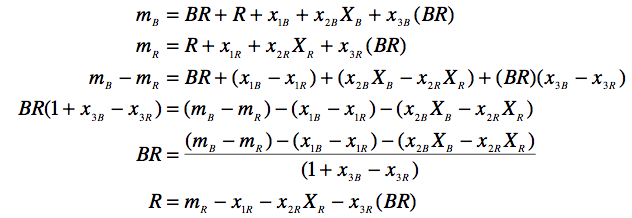


That sure looks like nice info for the serious observer. The Airmass calculator is great. However, is there another site that will take the airmass value and produce the spectral irradiance correction factors???
“rest assured tomorrow I’ll have a special online treat”
Pamela, I have been checking your blog almost every 30 minutes, for the last 24 hours.
You got my interest!
Now, when do we get the rest of the story?