 The other day, Astronomy Cast listener James S. sent us this really great question:
The other day, Astronomy Cast listener James S. sent us this really great question:
“Give me a lever long enough, a fulcrum strong enough and I’ll move the world” –Archimedes
No doubt both of you guys have heard the quote. My question is just how long of a lever would be needed, and where would the fulcrum need to be placed for an average human to lift the weight of the earth. If we assume that the weight of the Earth were being pulled on by a gravity equal to that of the earths gravity.
This is actually a really good question, and was way harder to work through than I had originally anticipated and requires a number of assumptions along the way.
First off, if the Earth is being pulled on by another Earth, where is that other Earth located? For instance, if another Earth where located 1 Earth diameter away (such that there is 1 Earth diameter between the two surfaces, and 2 Earth diameters between the two world’s centers), the Earth would be attracted to the second Earth as follows:
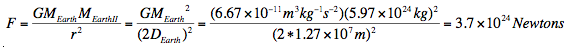
Placed on a gignormous balance, the Earth would weigh 8.3 x 10^23 pounds! Now lets say I can exert 100 pounds of force (~450 N) with my arms, I just need a lever that translates my 100 pounds of force into 8.3×10^23 pounds of output force. This is a torque problem:
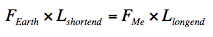
The only problem is, I don’t know how long either the long end or the short end of the lever is. That’s two unknowns and 1 equation. I’m going to make the assumption that if the end of the lever is just touching the Earth and is tangential to the surface, the closest the pivot could be is the visible horizon (about 5km from the surface).
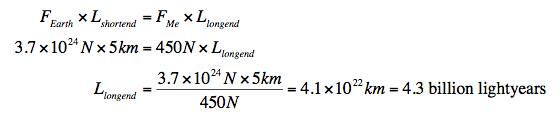
WOW! (Note: I’m assuming I’m pushing perpendicular and the other planet’s pull is pulling the planet perpendicular to the lever, and that I’m moving the Earth over such a small angle that I can ignore any change in angle of the force).
I’d known it was going to be a big number, but…
WOW! This means that if I move my end of the lever 1m, the Earth won’t have moved a meaningful distance. Let’s say I pushed my end of the lever 20 km/hr, 24 hours a day, totaling 240 km/day, I’d have to push my end for 9.3×10^13 years (way longer than the age of the universe!) to move the Earth 1 meter!
Now, part of the problem is, I have to over come not only the inertia of the Earth, but also the force that other planet is exerting on it. What if we remove that other pulling planet?
Now, I have to admit, that when I first thought about this several days ago, I figured I’d also real fast calculate this new number – the force needed to move the Earth assuming the universe consisted of nothing but me and the Earth, and a lever of negligible (but amazingly strong!) mass. I’ll stick the lever and the fulcrum in the same place. The only problem is, I don’t know either the force on the Earth from the fulcrum (I can make it anything!), or the length of the lever (again – two unknowns).
Well, I’m going to use basic rollar coaster 101 to solve this. Let’s speed things up, and assume that in my magical imaginary universe I have a space craft that will move my feet such that I keep up with the moving lever and always exert my 450 lbs of force on the lever (this is like pulling someone on rollar skates with your hands while you (don’t ever do this!) sit in the back of a pickup. You have to exert a certain force to pull them, but you don’t have to run or exert force to accelerate yourself. In my crazy imaginary universe, I’m going to say that as I slowly accelerate the Earth from rest and get it into motion, my acceleration can’t exceed 9gs (9 times the pull of gravity on Earth). At more than 9gs, people tend to pass out. This specific acceleration comes from my circular motion.

Which is a whole lot more reasonable, but still very silly.
Now here is where I ask you to be skeptical. Check my math. Look for bad assumptions. Look for things I missed. It’s late on a Sunday night and I’m doing math while watching Ghostbusters on Spike, which is showing a hilarious commercial with lizards doing the dance from Thriller (and some chick who really wasn’t necessary). I know myself well enough to know I likely enough I made a mistake. So – find it if it’s there 🙂
My students are so glad I’m not teaching a high lever class this semester (I’m teaching science foundations for education majors). In a class that covered gravity and circular motion, this would so totally be on the final…



Pamela, reading your post made me think of this xkcd comic – in a good way 😉
Why not simply F = ma ?
“..have to over come not only the “inertia” of the Earth, but also the “force that other planet” is exerting on it..” => aren’t they the same?
Hi Farstarz- If Earth sits all by its lonesome in the middle of nothing, it will experience no forces. If you then drop in a second planet, the Earth will experience a gravitational force toward the second planet, and that force is defined by F=GMm/r^2. The second planet will also experience an identical force in the opposite direction. Each of these forces will generate an acceleration that you can solve for by setting the force above equal to F=ma, and solving for ‘a’. Now, if I want to move the Earth, my force has to be great enough to overcome the other planets force, and great enough to move the Earth (overcome its desire not to move). This is roughly the difference between exerting the amount of force on a cat on tile needed to cause it to run in place while trying to escape, and exerting enough force to get it to slide backwards while it tries to run forward.
And Stuart – Thanks!
I never would have thought that it’s that tough!
Wow, and that’s only at 5km. The Earth isn’t all that moveable, afterall. 🙂
The coefficient of friction at the fulcrum, along with a few other things, might be a slight problem. 🙂
It is still a very cool result.
The Thriller Lizard commercial!! The only commercial I remember from the Superbowl this year! 😀
Ah. Ummm. Wait. Right. Back to science!
The (relatively) easy way to do it would be to build a catapult that would launch mass from the earth’s surface at escape velocity – it would have to be a human powered trebuchet if you wanted to narrowly interpret the fulcrum, lever and Archimedes prerequisite.
However, this would raise the question if the mass launched from the earth is still considered part of the earth, and so the centre of mass remains the same, did the earth move? (A question that has been asked more than once, but not in this context.)
A more elegant solution would be for Archimedes to stand outside during a meteor shower and bat away incoming bolides.
This shows that Archimedes anticipated the supposed work of Abner Doubleday by more than 2000 years. Syracuse has always been a great baseball town.
I like cheese 🙂
I have tried and no success. I re-calculate and re-calculate, it appears that I need to weigh about 50kg in the weightless environment. Not doable because I weigh 60kg on the planet earth — So the answer is: Down to earth and keep dreaming Archimedes – It’s good for you!
You are all wrong because the author correctly stated Archimedes’ quote but then turned right around in his next sentence and posed the question wrong. The author posed the question of what is needed to lift the weight of the earth. Archimedes said “move the earth”, not lift it. This is a huge difference. If you were trying to move a big round boulder that was too heavy to just pick up and move, would you look for a lever long enough to lift it’s entire weight or would you get a much shorter lever and simply wedge it under the edge of the boulder and roll it out of your way? Here is the answer to my question: If you were a physics teacher, you would engage yourself in laborious calculations trying to figure out the length of lever needed to lift the entire weight of the boulder against the earths gravitational pull, and the amount of distance the end of the lever would have to travel to result in a corresponding measureable amount of distance away from the earth’s surface. Whereas If you were a working person, you would simply get a much shorter lever, figure out the downhill side of the boulder (if any), wedge the lever under the uphill side, place the fulcrum a short distance from the boulder, and move it a minute fraction of the distance that the Professor would have to move his lifting lever, and then you would apply enough force to rotate the boulder from it’s resting position, at which point the earth’s gravitational pull in the downhill direction and the fact that a body in motion tends to stay in motion would then keep the boulder moving. The only thing you would have left to do is warn the physics professor not to stand on the downhill side of the boulder. All of these same principles that applied to the boulder would apply to moving the earth.
The problem is that the earth would have to be on a planet big enough to hold it in its gravity, billions of times more massive than Jupiter. Clever-clogs Archimedes would be crushed to the size of a grain of salt in a nanosecond.